Neural Network II | MLOps
This is the lecture for Neural Network II and MLOps.
Neural Network II
Here we go!
Symbolic differentiation
Many modern machine learning frameworks can compute gradients automatically, and this might lead to a large amout of intermediate variables which causes the increase of the computational expense and memory.
To solve this, some frameworks introduce dynamic computation graph which can avoid the case, and are more efficient than bp.
Mini-batch learning
Batch learning: Compute the gradients over all $N$ training samples and update
\[\begin{equation} \Delta \boldsymbol{w}^{(t)} = -\eta\nabla E \vert_{\boldsymbol w^{(t)}} \nonumber \end{equation}\]Use all data to compute the gradient during one iteration.
Mini-batch learning: Choose a subset
\[\begin{align} S_m & = \{(\boldsymbol{x_{i_1}, y_{i_1}}), ..., (\boldsymbol{x_{i_B}, y_{i_B}}) \} \nonumber \\ & 1\leq i_1 \le ... \leq i_B \leq B \leq N \nonumber \end{align}\]and update
\[\Delta\boldsymbol{w}^{(t)} = -\eta \sum_{(\boldsymbol{x}_n, \boldsymbol{y}_n)\in S_B}\nabla E^n \vert_\boldsymbol{w}^{(t)}\]Typically with a smaller learning rate $\eta \leq 0.1$.
Take a subset of all data during one iteration.
Vanishing gradient
Why we need to pay attention to the range of derivatives of activation functions? $Df$
In the neural network, activation function is applied to convey the messages. When training the network, we need to update the weights (parameters) by the loss function, which involves computing $\frac{\partial E}{\partial w}$ for each $w$.
Therefore, if the $\frac{\partial E}{\partial f}$ is too small, then, $\frac{\partial f}{\partial w}$ becomes much smaller in the back propagation and leading to “vanishing gradient” when increasing the number of layers.
\[\text{Target:} \frac{\partial E}{\partial w} = \frac{\partial E}{\partial f}\cdot\frac{\partial f}{\partial w}\]$\implies$ weights for front layers almost without updates due to the gradient
The selection of activation functions is important.
\[\begin{align} \text{Sigmoid:} & \frac{\partial E}{\partial f} = Dh \leq 0.25\nonumber \\ \text{ReLU:} & \frac{\partial E}{\partial f} = Dh = \begin{cases}0, & \text{if $a < 0$} \\ 1, & \text{if $a > 0$} \end{cases} \nonumber \end{align}\]Hence, ReLU is more widely-used and suitable for deep learning.
Efficient gradient-based optimization
Vanilla steepest-descent is usually not the best choice for (batch) gradient-based learning. (Batch Gradient Descent: BGD)

Even though BGD can find the global minimum, but due to its feature by using the whole batch, its expense for computation is extremely expensive and time consuming.

Basic problem

How to update the weights in the network to make the output close to the expected?
Figure 3 indicates the local shape for the loss function with respect to the weights. Plateau and Ravine.
In the plateau, the gradient for loss function is small, we need small step (learning rate) to reach the local minimum and this may lead the algorithm cannot continue to the global minimum. While for the ravine, its gradient is large which means we need to take larger step. However, it may lead to un-convergency because of the skip of the minimum. $\Leftarrow$ fixed step (learning rate)
To solve this, the idea is,
instead of directly using the magnitude of the partial derivative - to adjust the update in the direction of the partial derivative for each weight individually based on feedback from previous iterations.
If we directly use the magnitude of the partial derivative to update the weights in each iteration, we may end up with some issues such as convergence to suboptimal solutions or overshooting the optimal solution.This is because the magnitude of the gradient alone does not always provide us with the right direction to move towards the minimum of the loss function. $\Leftarrow$ Update the weights by taking the direction from previous iterations into account.
Rescaling by second raw moment I
Overview: It is a technique used in optimization algorithms, such as RMSprop and Adam, to adaptively adjust the learning rate for each weight in the neural network.
The second raw moment, also known as the variance, measures the spread of the gradient values for each weight over time. By rescaling the learning rate with the inverse square root of the variance, the optimization algorithm can effectively dampen the learning rate for weights with high variance (i.e., large fluctuations in the gradient values) and amplify the learning rate for weights with low variance (i.e., consistent gradient values). This can help the optimization algorithm to converge faster and more reliably.
Goal: Iterative minimization of $f(\boldsymbol{w})$
Taylor approximation:
\[f(\boldsymbol{w+\Delta w}) \approx f(\boldsymbol{w}) + \Delta w ^{\intercal} \nabla f(\boldsymbol{w})\]leads to update step
\[\boldsymbol{w}_i^{(t+1)} \leftarrow \boldsymbol{w}_i^{(t)} + \Delta {\boldsymbol{w}}^{(t)}\]in iteration $t$
\[\Delta \boldsymbol{w}^{(t)} = \arg\min_{\Delta \boldsymbol{w}} \{\Delta\boldsymbol w^\intercal \nabla f(\boldsymbol w^{(t)}) \text{ s.t. } \vert\vert\Delta\boldsymbol{w}^{(t)}\vert\vert \leq \alpha \} \implies Direction\]where $\alpha$ defines a trust region (in which we trust the approximation)
The goal of iteratively minimizing a function using the Taylor approximation.
The Taylor approximation is used to derive an update step in each iteration, which involves finding the optimal change in weight values while restricting their magnitude to a certain trust region defined by a parameter alpha.
The ultimate goal is to find the weight values that minimize the given function, and the rescaling by second raw moment is one technique that can be used to improve the convergence of the optimization process.
在这个方法中,我们使用Taylor展开来近似$f(\boldsymbol{w+\Delta w})$,然后将其代入到梯度下降的更新公式中,得到一个二次函数,进而利用二次函数的最小值来计算参数更新量$\Delta\boldsymbol w^{(t)}$。其中,通过引入一个trust region的概念,我们限制了参数更新的范围,使得更新量不会太大,也不会太小。这个trust region就是由$\alpha$来定义的。
Solution is co-linear with gradient and has maximum length:
\[\Delta \boldsymbol{w}^{(t)} = -\alpha \frac{\nabla f\left(\boldsymbol{w}^{(t)} \right)}{\vert\vert \nabla f\left(\boldsymbol{w}^{(t)} \right)\vert\vert} \implies Length\]Rescaling by second raw moment II
We have unbiased estimates $\nabla \widetilde{f}({\boldsymbol{w}^{(t)}})$ instead of $\nabla f(\boldsymbol{w})^{(t)}$, typically gradients computed on mini-batches:
\[\boldsymbol{\Delta w} = -\alpha \frac{\mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]}{\vert\vert \mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]\vert\vert} = -\alpha \frac{\mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]}{\sqrt{\mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)]^\intercal} \mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]}}\]Concretely, for neural networks $\nabla_i \widetilde{f}\left(\boldsymbol{w}^{(t)}\right)$ is the partial derivative of the error function estimate (the error over mini-batch) w.r.t. weight $w_i$ at iteration $t$
This section is discussing the second method of rescaling by second raw moment. In this method, instead of using the full gradient $\nabla f(\boldsymbol{w})^{(t)}$, we use unbiased estimates of the gradient, denoted as $\nabla \widetilde{f}({\boldsymbol{w}^{(t)}})$, typically computed on mini-batches.
The formula for updating the weights in this method is given by:
\[\boldsymbol{\Delta w} = -\alpha \frac{\mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]}{\vert\vert \mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]\vert\vert} = -\alpha \frac{\mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]}{\sqrt{\mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)]^\intercal} \mathbb{E}[\nabla \widetilde f(\boldsymbol{w})^{(t)}]}}\]This formula calculates the update step $\Delta \boldsymbol{w}$ as a scaled version of the expected value of the unbiased estimates of the gradient, divided by the square root of the expected value of the dot product of these estimates. In neural networks, the partial derivative of the error function estimate (the error over mini-batch) with respect to weight $w_i$ at iteration $t$ is denoted as $\nabla_i \widetilde{f}\left(\boldsymbol{w}^{(t)}\right)$.
Rescaling by second raw moment III

RMSprop | Adam
I don’t understand the following two. I will leave them in the below and figure them out later.


MLOps
First, what is DevOps?
DevOps integrates and automates the work of software development (Dev) and IT operations (Ops) as a means for improving and shortening the systems developement life cycle. (Courtemanche, Mell, Emily, Gills, Alxander, 2023)
Then, MLOps refers to the practice of applying DevOps principles and practices to the development, deployment, and management of machine learning systems.

ML Ops is a set of practices that aims to deploy and maintain ML systems in production reliably and efficiently.
Connections with DevOps

The diagram is emphasizing the idea that MLOps requires a combination of expertise and collaboration from these three fields. Machine learning is the core of MLOps, as it involves developing and training models, while DevOps is essential for deploying and managing those models in production environments. Data engineering is also critical for managing data pipelines and ensuring the quality and reliability of data used for training and inference. By bringing together these three areas, MLOps enables the end-to-end lifecycle of machine learning applications, from development and training to deployment and management in production.
Managing the data pipeline refers to the process of overseeing the flow of data from its source to its destination, ensuring that it is collected, processed, and stored properly. This involves tasks such as data ingestion, transformation, validation, cleaning, integration, and delivery.
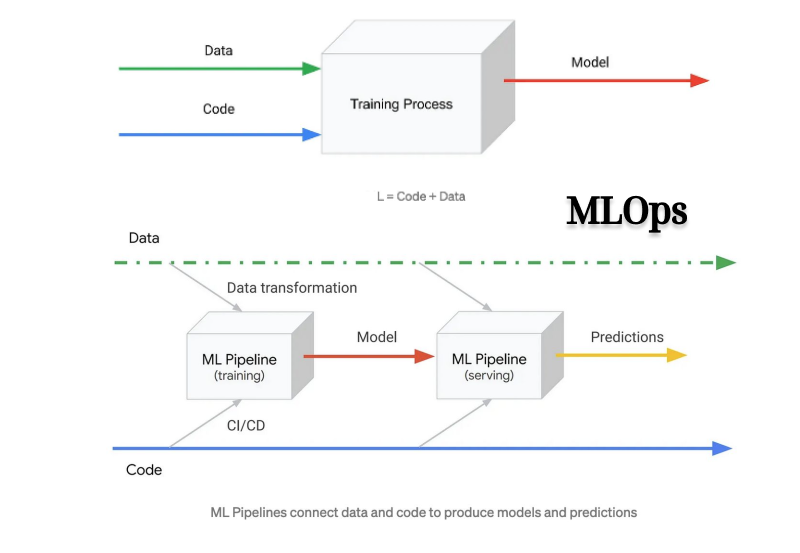
Here is the digram illustrate MLOps.

from https://towardsdatascience.com/ml-ops-machine-learning-as-an-engineering-discipline-b86ca4874a3f
My understanding is that the green line represents the Data Engineering techniques to do with data for ML systems. Blue line represents the DevOps including developing and deploying code for the ML systems. While the middle part is the Machine Learning to support the ML systems, consists of training and predicting. All these things connected together is called MLOps.
CI/CD stands for Continuous Integration/Continuous Deployment. It is a set of practices and tools that help automate the process of building, testing, and deploying software applications. The main goal of CI/CD is to reduce the time and effort required to deliver new features and updates to end-users by streamlining the development, testing, and deployment processes.
Continuous Integration involves automatically building and testing the application code every time changes are made to the code repository. This helps detect and fix issues early in the development process.
Continuous Deployment involves automatically deploying the code changes to production after successful testing and verification. This ensures that the latest version of the software is always available to end-users.
CI/CD can help teams to deliver higher-quality software faster and with more confidence, as it helps to catch errors earlier in the development process and reduces the risk of deploying buggy code to production.

from https://towardsdatascience.com/ml-ops-machine-learning-as-an-engineering-discipline-b86ca4874a3f
The table compares different practices in DevOps, Data Engineering, and MLOps. ML Ops is more advanced.
Reference
梗直哥丶 (2021) 【梯度下降】3d可视化讲解通俗易懂_哔哩哔哩_bilibili, _哔哩哔哩_bilibili. Available at: https://www.bilibili.com/video/BV18P4y1j7uH/?spm_id_from=333.337.search-card.all.click&vd_source=0d4296a4bf13df96761e313b112ab192 (Accessed: April 29, 2023).
Courtemanche, Meredith; Mell, Emily; Gills, Alexander S. “What Is DevOps? The Ultimate Guide”. TechTarget. Retrieved 2023-01-22.
Stefan Sommer. (2023) ADL 2023 - week 1 (Lecture Slide April 24, Apr 26 2023)