Neural Network

Recap of Neural Network

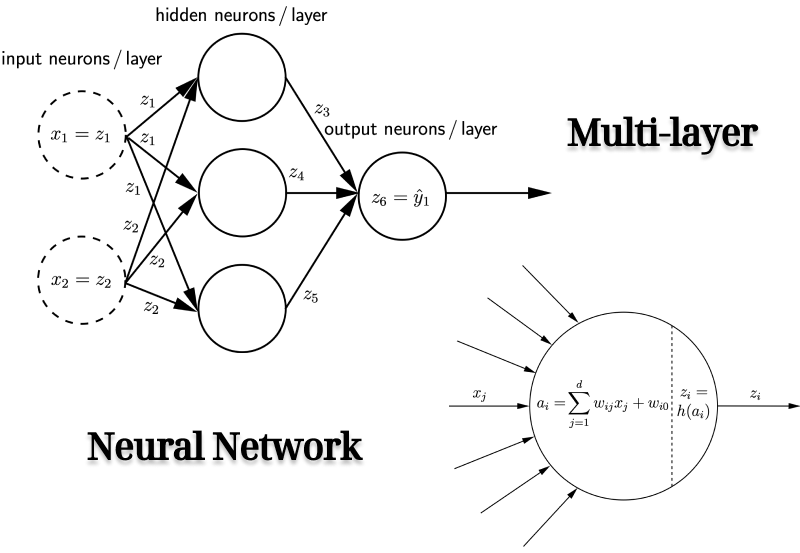
Neural networking learning

Using data to adapt (train) the parameters (weights) of a mathematical model.

Simple neuron models

image-20230425074015153
Figure 1. Single neuron with bias (Christian Igel, 2023)

Input is the vector $\boldsymbol{x}$ or $\vec{x}\in \mathbb{R}^d$.

\[\boldsymbol{x} = (x_1, ..., x_d)\]

Output of neuron $i$ be denoted by $z_i(\boldsymbol{x})$. Omit dependency on $\boldsymbol{x}$ to keep uncluttered.

\[a_i = \sum^d_{j=1}w_{ij} + w_{i0}\] \[z_i = h(a_i) = h\left(\sum^d_{j=1}w_{ij}x_j + w_{i0}\right)\]

We have an input with $d$ dimension for the neural network. For each node $i$, the first step is to calculate the integration which accepts all the incoming $x_i$ from $\boldsymbol{x}$ with corresponding weights $w_{ij}$, and then, add the bias $w_{i0}$. The second step is to activate the integration to be its output $z_{i}(\boldsymbol{x})$.

Some common activation functions

image-20230425081429722
Figure 2. Activation functions (Christian Igel, 2023)
\[h(a) = \mathbb{I}\{a>0\}\] \[h(a) = \frac{1}{1+e^{-a}}\] \[h(a) = \tanh(a)\] \[h(a) = \frac{a}{1+\vert{a}\vert}\] \[h(a) = \max(0, a)\] \[h(a) = \begin{cases} a, & a \geq 0 \\ \alpha (e^a - 1), & a < 0 \end{cases}\]

and $\alpha > 0$

Simple neural network models

Neural network (NN) is a set of connected neurons.

It can be described by a weighted directed graph. 1. Neurons are the nodes/vertices and numbered by integers $V = {0, 1, 2, …}$. 2. Connections between neurons are the edges $A$. 3. Strength of connection $(j, i)\in A$ from neuron $j$ to neuron $i$ is described by weight $w_{ij}$. 4. All weights are collected in weight vector $\boldsymbol{w}$.

To Feed-forward NNs: we do not allow cycles in the connectivity graph.

NN represents mapping

\[f: \mathbb{R}^d \to \mathbb{R}^K\]

parameterized by $\boldsymbol{w}: f(\boldsymbol{x; w})_i = \hat{y}_i$

In another representation with multiplications \*

\[f: \mathbb{R}^d \times \mathbb{R}^M \to \mathbb{R}^K\]

where $\mathbb{R}^M$ represents weights. Here, we omit the biases as they can be written together with weights? $w_{i0}$

In other words, $\mathbb{R}^M$ is the vector $w_{i0}, \text{all the weights}$. \*

Notation

$d$ input neurons, $K$ Output neurons, $M$ hidden neurons:

notation
Figure 3. Explanation of the Notations
\[\begin{align} V_{\text{input}} & = \{1, ..., d \} \nonumber\\ V_{\text{hidden}} & = \{d+1, ..., d+M \} \nonumber\\ V_{\text{output}} & = \{d+M+1, ..., d+M+K \nonumber \} \end{align}\]

Therefore, the whole set of vertices $V$ is,

\[V = \{0 \} \cup V_{\text{input}} \cup V_{\text{hidden}} \cup V_{\text{output}} = \{0, 1, 2, ..., d+M+K \}\]

Activation function of neuron $i$ is denoted by $h_i$,

\[h_i(a) = a\text{ for } i\in \{0\} \cup V_{\text{input}}\]

Typically $h_i \neq h_j$ for $i \in V_{\text{hidden}}$ and $j \in V_{\text{output}}$

Neuron $i$ can get only input from neuron $j$ if $j < i$, this ensures that the graph is acyclic $\leftarrow$ Feed-Forward NN

Activation of neuron $i>1$ is

\[a_i = \sum_{(j, i)\in A}w_{ij}z_j\]

Output of neuron $i$ is denoted by $z_i$

$z_i(a_i) = h_i(a_i)$

$z_0(\cdot) = 1$ ($w_{i0}z_0$ is the bias parameter of neuron $i$. Defintion?)

$z_i(\cdot) = x_i$ for $i$ for $i\in V_{\text{input}} = {1, …, d }$

Output of the network $f(\boldsymbol{x;w})$

\[f(\boldsymbol{x;w}) = \pmatrix{z_{M+d+1}\\z_{M+d+2}\\...\\z_{M+d+K}} = \pmatrix{\hat{y_1}\\ \hat{y_2} \\ ... \\ \hat{y_K}}\]

Sum-of-squres error

NN shall learn function

\[f: \mathbb{R}^d \to \mathbb{R}^K\]

$\implies d$ input neurons, $K$ output neurons

Training data

\[S = \{(\boldsymbol{x}_1, \boldsymbol{y}_1), ..., (\boldsymbol{x}_N, \boldsymbol{y}_N)\}, \boldsymbol{x}_i \in \mathbb{R}^d, \boldsymbol{y}_i\in \mathbb{R}^K, 1\leq i \leq N\]

$# \text{training} = N$.

Usually , linear output neurons:

\[h_i(a) = a \text{ for $i \in V_{\text{output}}$}\]

Sum-of-squares error

\[E = \frac{1}{2}\sum^N_{n=1}\Vert f(\boldsymbol{x}_n\boldsymbol{; w}) - \boldsymbol{y}_n\Vert^2\]

Back Propagation

Here we define $L$ represents loss, sum of the errors is below,

\[E(\boldsymbol{x; w}) = L\left(f(\boldsymbol{x;w}), \boldsymbol{y}\right)\]

To minimize $E$ by adjusting the weights $\boldsymbol{w}$, compute the $\nabla_\boldsymbol{w} E$.

Below is an concrete example to help understand the back propagation by SGD

The algorithm randomly generates $\boldsymbol{w}$, for each $w$ inside, using the following formula to update it such that coverage to the ground-truth.

\[w^+ = w - \eta \cdot \frac{\partial E}{\partial w}\]

Here, $\frac{\partial E}{\partial w}$ is the current $\nabla_w E$ which represents the range of the change for $w$ with respect to $E$, $\eta$ is the so-called learning rate (normally less than $0.1$) used to control the step.

The reason to compute the gradient is to estimate the true $\boldsymbol{w} \implies \nabla_w E$.

Chain Rule

Assume $y = g(x), z = f(y)$, then, $z = h(x), h=f\circ g$ where $h$ is a compound function.

We know that,

\[\frac{d_y}{d_x} = g'(x), \frac{d_z}{d_y}=f'(y)\]

By calculus,

\[h'(x) = \frac{d_z}{d_x} = \frac{d_z}{d_y} \cdot \frac{d_y}{d_x}\]

This is the case of single variable, but it suits for the multiple variables.

Example of BP

image-20230425104734735
Figure 4. Concrete Feed-Forward NN example for back propagation (HexUp, 2018)

Here we have two layers, there are two neurons $x_1 = 1, x_2=0.5$ in the input layer, two neurons $h_1, h_2$ in the hidden layer, and the final neuron $y$ for output layer. Each neuron gets fully connected.

Given that the ground-truth values for $\boldsymbol{w}$,

\[w_1 = 1, w_2 = 2, w_3 = 3, w_4 = 4, w_5 = 0.5, w_6 = 0.6\]

In this setting, the true value for $t = 4$.

To mock a process of back propagation, assume we only know $x_1 = 1, x_2 = 0.5$ and the target $t = 4$.

First, randomly generates the weights,

\[w_1 = 0.5, w_2 = 1.5, w_3 = 2.3, w_5 = 1, w_6 = 1\]

Then, conduct the forward pass,

\[\begin{align} h_1 & = w_1 \cdot x_1 + w_2 \cdot x_2 = 1.25\nonumber \\ h_2 & = w_3 \cdot x_1 + w_4 \cdot x_2 = 3.8\nonumber \\ y & = w_5 \cdot h_1 + w_6 \cdot h_2 = 5.05\nonumber \\ E & = \frac{1}{2}(y-t)^2 = 0.55125\nonumber \end{align}\]

Sequently, do the backward pass. $y$ is the expected value from NN, and the target true is $t = 4$, we need to update $w_5$.

\[\frac{\partial E}{\partial w_5} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial w_5}\]

Because $E = \frac{1}{2}(t - y)^2$, therefore,

\[\begin{align} \frac{\partial E}{\partial y} & = 2 \cdot \frac{1}{2} \cdot (t-y)\cdot (-1)\nonumber \\ & = y - t\nonumber \\ & = 5.05 - 4\nonumber \\ & = 1.05\nonumber \end{align}\]

For $y = w_5 \cdot h_1 + w_6 \cdot h_2$,

\[\frac{\partial y}{\partial w_5} = h_1 + 0 = h_1 = 1.25\]

By the chain rule,

\[\begin{align} \frac{\partial E}{\partial w_5} & = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial w_5} = (y-t)\cdot h_1\nonumber\\ & = 1.05 \cdot 1.25 = 1.3125\nonumber \end{align}\]

Updating $w_5$ by using previous formula, where $\eta = 0.1$,

\[\begin{align} w_5^+ & = w_5 - \eta \cdot \frac{\partial E}{\partial y}\nonumber \\ & = 1-0.1 \cdot 1.3125\nonumber \\ & = 0.86875 \nonumber \end{align}\nonumber\]

Update the $w_6$ in the same steps $\implies w_6^+ = 0.601$

Move to $w_1, w_2, w_3, w_4$, take the computation for $\nabla w_1 E$ as an example,

\[\frac{\partial E}{\partial w_1} = \frac{\partial E}{\partial y} \cdot \frac{\partial y}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_1}\]

$\frac{\partial E}{\partial y} = y - t$ has already been computed and for $y = w_5 \cdot h_1 + w_6 \cdot h_2$,

\[\frac{\partial y}{\partial h_1} = w_5 + 0 = w_5\]

By $h_1 = w_1 \cdot x_1 + w_2 \cdot x_2$,

\[\frac{\partial E}{\partial w_1} = x_1 + 0 = x_1\]

Therefore,

\[\frac{\partial E}{\partial w_1} = (y-t) \cdot w_5 \cdot x_1\]

Update $w_1$, and similar for the rest.

\[w_1^+ = 0.395, w_2^+ = 1.4475, w_3^+ = 2.195, w_4^+ =2.9475\]

Conduct the forward pass again,

\[y^+ = 3.1768, E^+ = 0.3388 < E\]

Repeating the steps above, then that is the back propagation.

To get connection with our lectures,

\[\begin{align} \nabla_w E = (D_wE)^\text{T}\nonumber \\ D_w E = D_1 L \cdot D_w f\nonumber \end{align}\]

Here,

\[D_wf = \pmatrix{\frac{\partial f^1}{\partial w^1} & ... & \frac{\partial f^1}{\partial w ^M}\\... & ... & ... \\ \frac{\partial f^K}{\partial w^1} & ... & \frac{\partial f^K}{\partial w^M}}, \text{ Jacobian Matrix}\]

We can do the following derivation. We already know that $f(\boldsymbol{x; w})$ can be written like below,

\[f(\boldsymbol{x; w}) = \boldsymbol{h}^N\left(\boldsymbol{w}^N \boldsymbol{h}^{N-1}(\boldsymbol{w}^{N-1}...\boldsymbol{h}^1(\boldsymbol{wx}) \right)\]

Then, $D_wf$ could be written as,

\[D_wf = D\boldsymbol{h}^ND\boldsymbol{w}^ND\boldsymbol{h}^{N-1}....D\boldsymbol{h}^1D\boldsymbol{w}^1\]

Each item above is a matrix. Then, compute the $\nabla_wE$.

\[\begin{align} \nabla_w E & = (D_w E)^\text{T} = (D f)^\text{T} (D L)^\text{T}\nonumber\\ & = (Dw^1)^\text{T}(Dh^1)^{\text{T}} ... (Dw^ N)^\text{T}(Dh^ N)^\text{T}(DL)^\text{T}\nonumber \end{align}\]

As the last weights always need to be computed than the previous, then, that is the reason for calling back propagation.

Lecture written-note

151711682420321_.pic
Figure 5. Hand-written from lecture (Stefan, 2023)

Reference

Christian Igel. (2023). Neuron Networks. Deep Learning. UCPH

HexUp. (2018). Back Propagation（梯度反向传播）实例讲解. 知乎专栏. https://zhuanlan.zhihu.com/p/40378224

Stefan Sommer. (2023). Recap of Neural Networks. Advanced Deep Learning. UCPH